How to Conduct a Repeated Measures MANCOVA in SPSS
 Jeremy Taylor |
Jeremy Taylor |  Friday, April 20, 2012 at 1:35PM
Friday, April 20, 2012 at 1:35PM Let's get started:
Repeated-Measures MANCOVA is used to examine how a dependent variable (DV) varies over time, using multiple measurements of that variable, with each measurement separated by a given period of time. In addition to determining whether the DV itself varies, a MANCOVA can also determine wether other variables are predictive of variability in the DV over time. If that wasn't crystal clear, don't worry, just keep reading.
Repeated-Measures MANCOVA Example:
In our example, your local stats store Stats "R" Us launched a marketing campaign, with three different strategies (variable name: promo; value labels: Strategy A, Strategy B, Strategy C). Stats "R" Us launched campaigns in markets of three different sizes (variable name: mktsize; value labels: Small, Medium, and Large), and measured the sales in each store every three months over the course of one year (4 time points; variable names: sales.1, sales.2, sales.3, and sales.4; see data below).
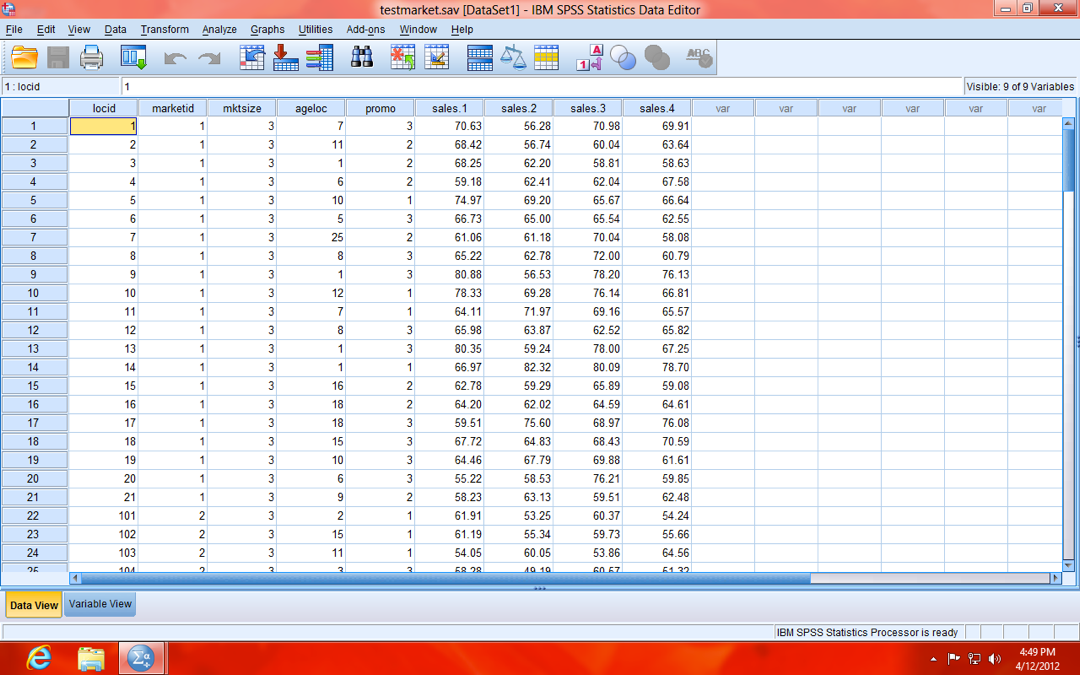
NOTE: Sales are scaled in "thousands" (e.g. 70.63 is actually $70,630). Also, your data should be in person-level (a.k.a. "wide") format (as opposed to person-period, a.k.a. "long", format), meaning each row of data is a single case (store, in our example). If it were in person-period (long) format, each case (store) would have the number of rows equal to the number of repeated measures (four, in our example), because the repeated measures (sales.1, sales.2, sales.3, and sales.4) would be stacked to form a single variable (Sales). Here is a useful resource for converting data between the two forms: CLICK HERE FOR INFO ABOUT CONVERTING DATA FORMS.
To begin your analysis using the SPSS drop-down menus, click on: Analyze > General Linear Model > Repeated Measures... (1, below)

In the Repeated Measures Define Factors dialogue window, do the following:
- Replace the default Within-Subject Factor Name, which is factor1, with your own name for the concept of time. I've chosen to use the name Time (1, below).
- Type the number of times your DV was measured (how many DV variables you have) in the Number of Levels box (2, below) and click the "Add" button.
- Choose a name for your DV (the variable that is measured repeatedly), and type it in the Measure Name box. I chose the name Sales (3, below).
- Click the "Add" button again (4, below).
- Click the "Define" button (5, below).




In the Repeated Measures dialogue window that appears next, move the four sales variables (1, below) to the Within-Subjects Variables (Time) box (2, below).
NOTE: Be sure that they stay in the same order (Sales.1, Sales.2, Sales.3, and Sales.4).


Next, move both promo and mktsize to the Between-Subjects Factor(s): box (1, below).
NOTE: Both promo and mktsize were placed into the Between-Subjects Factor(s) box because they are categorical variables (discrete variables). Continuous variables (scale variables) would go into the Covariates box (2, below).

Next, click on the "Model" button (3, above).
In the Repeated Measures: Model dialogue window (1, below), you can specify your model. In other words, you can choose which variables have "main effects" on the DV (individual predictors), and which variables might interact with each other to predict the DV. The default option is the Full factorial (2, below), which will examine every variable's main effect, as well as every possible interaction among all variables.

We'll stick with Full factorial for today. However, if you wanted build your own model, you can choose Custom (1, below), and then use the Build Term(s) tool (2, below) to specify what kind of effects/interactions you want. Again, in this example, we'll stick with Full factorial (2, above). To exit this dialogue window, click the "Continue" button.

Next, you'll need to click on the "Contrasts" button (1, below). In the Repeated Measures: Contrasts dialogue window that appears, you can change each factor variable's type of contrast. I recommend leaving the Time variable with its default contrast "Polynomial" (2, below), and changing both promo and mktsize to "Simple" and "First". To change each, you must select "Simple" from the list, click on "First", and then click on the "Change" button (3, below).

Next, click on the "Plots" button (1, below). In the Repeated Measures: Profile Plots dialogue window that appears (2, below), you can choose what graphs you'd like to see. In repeated measures models, I like to produce plots with Time on the Horizontal Axis (x-axis; 3, below) and my factor variables as Separate Lines (4, below).
NOTE: The reason you don't see anywhere to specify the vertical axis (y-axis), is that the DV (i.e. Sales) is assumed to be on the y-axis in this dialogue window.
As you can see, in our example I've made a Time-by-Factor plot for each of the factors in our model (promo and mktsize).

If you'd like to get Post Hoc comparisons of the DV (comparing between each of the factor levels, respectively), click on the "Post Hoc" button. Once in the dialogue window:
- Move the factors from the Factor(s) box (1, below) to the Post Hoc Tests box (2, below).
- Choose the type of Post Hoc test to use, and place a check-mark in its respective box (you can choose more than one). The most commonly used is Tukey's, which I've chosen below (3, below).
- Click the "Continue" button.

I also recommend clicking on the "Save" button (1, below), and choosing Predicted Values:Unstandardized (2, below) and Residuals: Unstandardized (3, below) in the Repeated Measures: Save dialogue window.
NOTE: By checking these two boxes, your analysis will now produce two new variables in your dataset, called PRED_1 (Predicted) and RES_1 (Residual), which can be used to produce graphs after analysis (if you choose). We will not cover this in this tutorial.

Back at the main Repeated Measures dialogue, you can either click "OK" (1, below), to execute the analysis, or you can click "Paste" (2, below), to paste the analysis commands into a syntax window. I recommend choose the "Paste" option, as that will allow you to more easily re-create the analysis later.
Below is the syntax window, with the various commands of the analysis, which you specified while going through the dialogue windows. Over time, you may learn to use syntax exclusively, bypassing the need to use the dialogue windows. Learning syntax can dramatically improve your efficiency, especially when you need to create a lot of different types and/or iterations of analyses.

To execute the commands in the syntax, simply highlight all the text you want to run, and push the green play button (1, above). Alternatively, you can use the menus: Run > Selection.
Interpreting Output/Results
There is a lot to digest in the output file that results from an analysis, so we'll stick to the basics. Below is the Descriptive Statistics table, which simply shows the Mean (1, below), Standard Deviation (Std. Deviation; 2, below), and sample size (N; 3, below) for each DV, broken-down by all subgroups of your factors (promo and mktsize).

The next table we'll examine is the Mauchly's Test of Sphericity. This test essentially determines whether the variance of the difference between each pair of repeated measure (of your DV) is approximately equal. This is a bit of an over-simplification, but it'll work here. For our purposes, we just need to be concerned with whether it is significant or not (1, below). If it is NOT significant (i.e. Sig. is greater than .05), then sphericity can be assumed (more on that soon). If it IS significant (i.e. Sig. is less than .05), then sphericity can not be assumed (more about why we care, in a moment).
NOTE: I know I said earlier that we wouldn't deal with assumptions today, but this is an exception, because it directly determines how we interpret the next table...
In our example, we CAN NOT assume sphericity (p=.003).

The reason we want to note whether sphericity can be assumed, is that it directly determines how we interpret our next table, the Tests of Within-Subjects Effects table (1, below). For each effect in our model, there are four estimates present (2, below). If sphericity CAN be assumed, then we can reference the first estimate, aptly labeled Sphericity Assumed. If sphericity CAN NOT be assumed, then we'll want to reference one of the other three (the differences between them is somewhat esoteric, but I typically choose Greenhouse-Geisser). In either case, we reference the Sig. column (3, below) to determine whether our effects are significant.
In our example, we see that we had no significant effects. Since we could NOT assume sphericity, the Greenhouse-Geisser test tells us that Time was not a significant predictor of Sales (i.e. there was no overall positive or negative trend in Sales in the company as a whole), F(2.743, 340.097)=.743, p=.516, ηp2=.006.
We also see that neither promo F(5.485, 340.097)=.660, p=.668, ηp2=.011, nor mktsize F(5.485, 340.097)=1.048, p=.391, ηp2=.017 interacted with Time to predict trends in Sales. Additionally, there was also no significant three-way interaction between Time, promo, and mktsize F(10.971, 340.097)=.940, p=.502, ηp2=.029. Take note of how I report those statistics , as it is necessary for APA format.

The next table was produced because we chose the "Polynomial" contrast for Time earlier. It is very useful in case non-linear relationships exist in your data. More specifically, it determines whether there is a Linear or a non-linear relationship exists, such as Quadratic or Cubic (1, below). The more nuanced differences between these effects is beyond the scope of this blog, but Notre Dame's Dr. Richard Williams explains it well in his page on Non-linear Relationships.

The Tests of Between-Subjects Effects table (below) shows whether the factors were associated with differences in Sales (overall, as opposed to whether there were differences in trends).
Results indicate that both promo F(2, 124)=12.837, p<.001, ηp2=.172 and mktsize F(2, 124)=15.085, p<.001, ηp2=.196 were predictive of differences in Sales (overall), while the interaction between the two was not significant F(4, 124)=.186, p=.945, ηp2=.006. These results may seem a bit confusing, because they are in direct contrast to the within-subject effects reported earlier, but it will become more clear when we examine the plots of the effects next.

The plot below shows the mean Sales at each of the four data collections, for stores using each of the three promotional Strategies (three lines). The graph demonstrates that there are distinctions between sales numbers of the three strategy groups, as (Strategy A was highest at every time point and Strategy B was lowest at every time point). However, since the trend for each group (if you were to impose a trendline across the four points for each group) is not dramatically different (and because the interaction term was not significant), we can't clearly say that one promotional strategy is superior to the others.
Since, the differences between groups at time pionts 2, 3, and 4 are largely reflective of the differencs that existed at baseline (time 1), it seems that differences that exist between groups are more likely attributed to differences in the composition of the groups, rather than differences in the promotional strategy. The graph for mktsize can be interpreted in the same way as promo.

This graph further shows how it is better to examine within subject differences when analyzing change over time, as plotting those effects makes the lack of differences in trend between promo groups more clear. Thanks for reading and please leave comments and/or questions!Editorial Note: Stats Make Me Cry is owned and operated by Jeremy J. Taylor. The site offers many free statistical resources (e.g. a blog, SPSS video tutorials, R video tutorials, and a discussion forum), as well as fee-based statistical consulting and dissertation consulting services to individuals from a variety of disciplines all over the world.


Reader Comments (27)
I love you!
LOL, thanks! I'm glad I helped!
Hello, thanks for the nice description of repeated measures! Very easy to follow..
I have a question with respect to my study in conducting a GLM repeated measures regression.
You have treated two independent variables to reflect differences in the dependent (sales) variable over time. Although my study also contains a dependent variable measured at 4 different time periods (2004, 2005, 2006 and 2007).
Although every years dependent variable is associated with 3 independent variables that belong to the same year.
So X1, X2, and X3 of 2004 will predict Y 2004
And X4, X5 and X6 of 2005 will predict Y 2005
and so on...
Do you recommend to create the data sheet in the wide way.. therefore treat each case as a single case (firm) and create the variables for each year, or in the long way?
In addition, for regression I always learned to transform categorical variables into dummies to use them as covariates, which would mean not to use the between-subject effects.
Also if I specify that my within-subject effect factor is 'performance', as dependent variable, with 4 levels (for all 4 years) and I include only the independent variables of 2004 the output creates estimate parameters predicting performance not only for 2004 but also for all other years based on the covariates of 2004. It would not make sense to interpret relations that go beyond the initial time period that is examined, can I specify into the model not to estimate these parameters?
Thanks in advance!
Thanks for the great question, Ruud!
If I understand correctly, you want to analyze the change in your DV (perhaps performance) over time (4 time points), while holding a time-varying covariate(s) constant, and while evaluating the predictive ability of several time-varying IVs. Is that correct?
If so, I hope your sample size is fairly large, because that is shaping-up to be a very complex model, which will require a large sample to be adequately powered. Assuming that is the case, I would recommend using a growth curve model (GCM). Unfortunately, SPSS isn't good for doing GCM, although they do make a program that does it (called AMOS). I prefer using either Mplus or R (with R being my favorite). I'll paste links to info on either option below.
I prefer using R (the "lavaan" package in particular), because it has all the functionality you'd get from other software, and it is FREE! Mplus and AMOS are definitely not free.
Here is a link to info about Mplus: https://www.statmodel.com/orderonline/categories.php?category=Mplus-Software
Here is a link to get R (on any platform, i.e. PC or mac): http://cran.r-project.org/" target="_blank">http://cran.r-project.org/
Here is a link to the "help" document/Users manual for R: http://jeremyjaytaylor.squarespace.com/storage/blog-files/R%20Help.pdf
Here is a link to get the "lavaan" package for R: http://cran.r-project.org/web/packages/lavaan/index.html
Here is a link to the "help" manual/documention fo rthe lavaan package: http://jeremyjaytaylor.squarespace.com/storage/blog-files/lavaan.Intro.pdf
Thanks for the help!
Although, I am not quite sure if that is exactly what I intend measure. I know some multivariate analysis, although I am definitely not an expert.
The sample of my thesis is 36 airline carriers (firms), so quite small. Comparative studies that I can show you use generalized least squares regression model, in which all cases are included into the model for each year. This would mean that my dataset would contain 36 times 4 (for every year) cases = 144 cases. In order to capture the time dimension, such studies take time as dummy variables into account, which would mean that I can use a dummy for 2004, 2005 and 2006 with the year of 2007 as reference group.
My teacher in statistics thought that such studies use mixed models for conducting the analysis, although he didn't recommended this method for me because of the complexity associated with it. Therefore he thought that GLM repeated measures would fit my data.
I don't know if this information provides new insights to your thoughts...
Thanks in advance!
Ruud,
It's very difficult to examine longitudinal data with a sample size as small as 36, particularly with only 4 time points. If you have additional years of data available, you could obtain more reliable estimates of change, increasing your power, even with a small sample size. As it is, I think I'd probably still attempt a growth curve model, perhaps turning to a repeated measure GLM as a backup.
Hello! Good description. I have a question, hoping you could help me. I want a RM Mancova, but when I move covariates in the covariates box, I can't perform a post hoc test. How can I see where the differences exactly are?
Thanx in advance!
Hey Marjie,
Great question, Marjie! Are you including interactions in your analysis? I'm guess that you are, because that is the only time post hocs would be necessary. If so, are both variables that are used in the interaction term continuous?
Hi there. This is very helpful. Thank you! I am running a MANCOVA with Reaction Time (RT) as the DV and four IVs each with two levels. I would like to run a series of Paired Sample t-tests on the predicted variables created in order to compare means for certain categories after the covariates have been factored out of the analysis. I want to make sure that the "new predicted variable" obtained by choosing the Unstandardized Predicted variable in the SAVE option gives me the modified values for my DV after the covariates have been factored out of the regression. Is this correct?
Thanks in advance!
Hi,
I have two DV's (positive affect and negative affect) which were measured at three time points (baseline, time 1, time 2) in a repeated measures design (the same participants reported positive/negative affect at 3 time points: baseline, time 1 and time 2. I want to see if there is a significant increase in either positive or negative affect (or both!) from the time 1 to time 2 whilst controlling for baseline positive/negative affect. I think I need to do a repeated measures MANCOVA... is this correct? I tried to follow your instructions (which are really good) but I still got confused :( A few silly questions: I'm wondering how many levels to give my within subjects factor? I have 2 DV's (positive and negative affect) but they are measured at 2 time points (time 1 and 2) so do I put 4 levels for my within subjects factor? (i.e. Time 1 positive affect, Time 2 positive affect, Time 1 Negative affect, Time 2 Negative affect). And does it make most sense to put baseline positive and baseline negative affect into the covariates box or to put them in the within subjects variables box?
Thanks, any help will be much appreciated!
I'm not sure I understand completely, but I think you are on the right track... you could run the covariates in a separate model and then "Save" the residuals, to partial-out the portion of the DV explained by the covariates...
Hi.
Thank you for posting this. I have multiple DV's, two time-points and two between-subject factors (one with 3 levels [Drug 1, Drug 2, Drug 3] and one with 2 levels [male, female]). However, my groups are not similar at baseline (some of the DV's have statistically significant differences at baseline). How can I account for the baseline differences when using repeated measures Manova? I would appreciate your reply! Thanks in advance.
I'm not sure I understand the question. By including the variables as covariates in the model you are "accounting" for differences that may exist as a function of those variables.
Thanks for a great description. I was able to follow along and run my RM-MANCOVA but I am having some trouble figuring out what to do with the covariates. Here are the components of my model
3 DVs (Aggression, Relational Aggression, Prosocial Behavior)
1 Repeated Measure IV (Grade: 7th and 9th)
2 Between Subject IVs (Gifted: Not Gifted vs Gifted ; Sociometric Status: Popular, Average, Controversial, Neglected, Rejected)
3 Covariates (Gender (0=Female); Race (0=white); Family SES (continuous)
I am most interested in the main effects and interaction between my 2 Between Subject IVs (Gifted, Sociometric Status) on my 3 DVs and whether this changes from 7th to 9th Grade (so the 3 way interaction between grade, gifted and sociometric status) while accounting for my 3 covariates.
However, when I run either a Full Factorial or Custom model I get so many extra main effects and interactions with my covariates that I am not interested in. I am intrigued by your previous post stating "covariates in a separate model and then "Save" the residuals, to partial-out the portion of the DV explained by the covariates". Can you elaborate more on how I would do this and whether there are any citations I could reference in a manuscript so the reviewers know this strategy is kosher.
Would I run a separate univariate ANOVA for each DV with Gender and Race as "Fixed Factors" and Family SES as the covariate and then select "Save" and select unstandardized or standardized residuals (any advice on which one?).
Then I would use the residual values in my RM-MANOVA and run everything the same except leaving out the 3 covariates?
Thanks!
Before I respond further, allow me to confirm my understanding: do you have 3 years of data for all variables? You said "repeated measures", so that gave me that impression, but I'm not sure...
So we have two years of data for the dependent variables. So each person has 7th and 9th grade data for Overt Aggression, Relational Aggression and Prosocial behavior. So grade (or we could call it "Time") is the RM variable with 2 levels. Does that help? Thank you so much!
Hello
Thank you very much for your explanation.
Could you please give some advice regarding the following?
I did a study on te effects of an intervention in participants brain waves and compared it to a control intervention, in the same peolpoe, one week later.
So, participants brain waves were measured for 10 minutes to assess baseline values and after this the intervention started and was applied for 15 minutes. Brain waves were assessed every 5 seconds and summed in a single index ranging from 0-100(absence of brain activity-full alertness)
In this way I intended to compare the effect of the experimental intervention to the control intervention but correct it also to baseline (10 min. pre intervention brain waves)
I tried to use the Ancova(general linear model -> repeated measures) but i found the following problem:
First of all, the maximum number of levels is 99. I have 300 hundred observations. How could i accoodate this?
Also, when i put the Baseline values as a Covariate, it doen't change the results. What is the problem? Would the be a better way of doing this? Can I use a continuous variable as a covariate?
Thank you very much in advance for your help
Nuno
I managed to generate imputed repeated measure data sets in spss but do not know how to use
those imputed results to perfrom repteated measure anova in spss.
Hi Pam!
I recommend checking out the Imputation section or and/or SPSS topics sections of the discussion forum:
http://www.statsmakemecry.com/statistics-discussion-forum/
Basically, if the data is split by dataset after imputation, then you should be able to run analysis as normal and SPSS will produce estimates for each imputation dataset and a set pooled estimates (for analyses that support multiple imputation (MI) in SPSS. For those that are not supported by SPSS for MI, pooled estimates and standard errors would need to be calculated (see forum for this also).
If you have additional specific questions along the way, feel free to post questions in the forum also! I hope this is helpful!
Hello there,
thanks for the interesting post :)).
I had some questions regarding RMANCOVA.
First of all can i use it when i am actually interested in my continuous predictor (i don't want to just control for it) ?
In my study, i have a repeated measures design and i want to see whether people's performance on a task was influenced by the type of task (3 levels-within), the type of stimulus (2 levels-within) and trait anxiety measured at the beginning of the experiment (continuous predictor). i am of course interested to see if my continuous has a main effect on performance but also if it interacts with my 2 IVs.
Is it correct to add the continuous predictor as a covariate ?? or should i do multi-level modeling?
And if it is the correct analysis, what do i do when i have a significant interaction between my IV and the co-variate?? how do i examine that???
Thank you in advance for all the help,
Elena
(stats do make me cry)
about to cry.
i have time 1 and time 2, 3 dvs, and 2 covariates. multivariate result indicates no significance for time, and both interaction terms for time and covariates. HOWEVER, when i look at the between subject above the within subject under multivariate test, one of the covariates is significant. does that mean that variable impacts all dvs in some way but not specified? so then, i looked at tests of between subject effects and saw that for one of the covariates, two of the dvs were significant. what does such result mean?? thanks in advance for your help. i really appreciated.
Elena and Jane.
These are great questions, but please post them in the discussion forum, as others can benefit from your question and the answer (and you are likely to get a quicker response also).
http://www.statsmakemecry.com/statistics-discussion-forum/
This really was a life saver! Also, id like to know if mancova can only be done on only the very recent versions of SPSS (namely; Version 20 &/or 21)
or ones older than those, aswell?
To my knowledge, this has been possible on SPSS for a long time, but it is possible that it required an add-on in previous versions, I'm not 100% sure...
Please, could someone guide:
MY design is 2 (pre and post test)(within) X3 (levels of interventions)(between) mixed factorial design. I have three Dependant variables and 2 covariates (gender and class). I am looking for is 'there would be an increase in the compassion of compassion group(3rd level of intervention) than 1st and 2nd levels of intervention'. I also want to look into 'an increase in POST test scores after intervention'. Would MANCOVA analysis answer my both questions?
Thought you'd like to know your work was copied here: https://statworkz.com/2016/04/11/how-to-conduct-repeated-measures-mancova-in-spss/
Hello,
I came across your blog looking for another type of analysis.
Why does the title of your analysis say "repeated measures MANCOVA" if your design is, in fact, straight up "mixed design ANOVA" with zero covariates?
There are designated names for analyses, making up new names only confuses readers.
With respect !